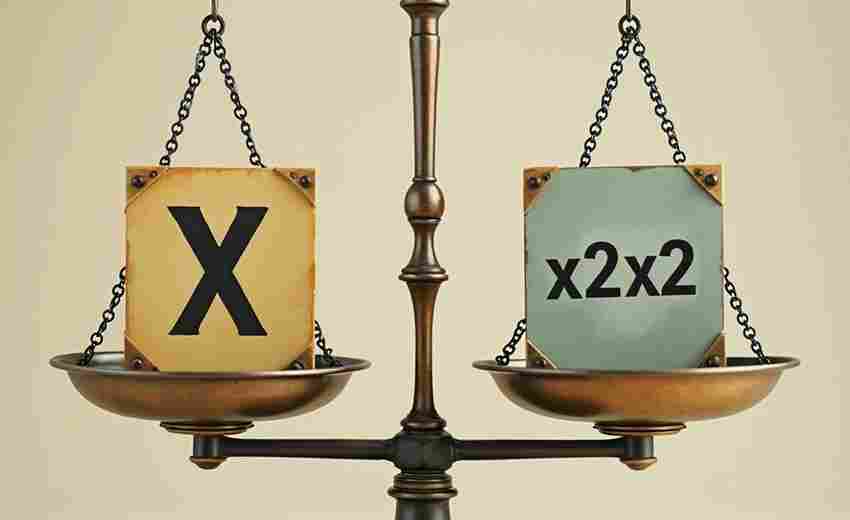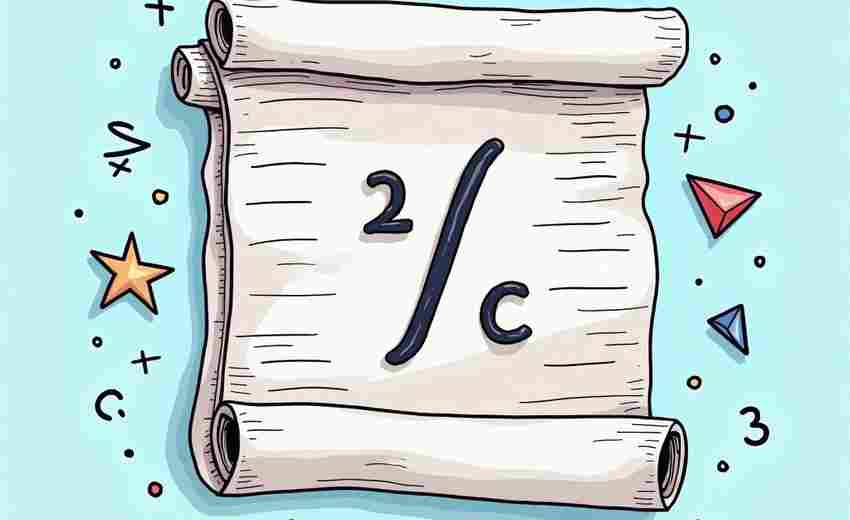二分之一在几何图形中的面积平分应用

---

---

几何图形中的面积平分问题，始终是数学与现实世界对话的重要桥梁。当一条直线将矩形切割为面积相等的两部分时，这种看似简单的操作背后，蕴含着深刻的数学原理。在建筑设计中，工程师需要精确分割地块；在机械制造领域，平衡配重的计算都印证着等面积分割技术的实用性。其中，二分之一作为最基本的比例关系，在几何分割中展现出令人惊叹的普适性。

对称性与等积构造

任何具有对称轴的图形都天然具备面积平分的可能性。以标准矩形为例，通过几何中心作垂直于长边的直线，总能将面积均分。这种特性在古希腊建筑中得到完美应用，帕特农神庙的立柱间距就是利用轴对称实现的视觉平衡。但并非所有对称轴都能直接应用，当图形存在多个对称轴时，需要结合重心坐标进行综合判断。

法国数学家庞加莱在《科学与方法》中指出："对称性不仅带来美学愉悦，更是解决实际问题的钥匙。"圆形的无限对称轴特性使其成为最易分割的图形，但将这种方法移植到不规则图形时就会遇到挑战。现代测绘技术中，通过建立极坐标系并计算积分面积，工程师能精确找到通过重心的任意角度平分线。

动态分割中的比例平衡

当固定面积的图形进行形变时，保持面积二分需要动态调整分割线。等腰三角形顶角变化时，平分线位置必须同步调整才能维持面积相等。这种动态平衡关系在液压系统的压力平衡装置中尤为重要，德国机械工程师冯·卡门曾在其流体力学研究中建立过相关数学模型。

抛物线拱桥的设计完美展现了这个原理。当桥面载荷变化时，通过调整拱形曲线的参数，既能保证结构强度又能均衡两侧压力。2018年清华大学团队在悬索桥研究中发现，将主缆锚固点设计为动态可调结构，可使桥梁在温差形变时自动保持载荷均衡，这项技术已应用于港珠澳大桥的建造。

分形几何的递归分割

曼德布罗特提出的分形理论为面积分割开辟了新维度。科赫雪花的每级迭代都严格遵循面积倍增规律，其边界线本身就成为天然的分割工具。这种特性在微电子领域得到应用，英特尔公司在芯片散热层设计中采用分形结构，使导热面积精确控制在预定比例。

但分形分割的数学验证充满挑战。2015年《自然》杂志刊载的论文显示，谢尔宾斯基三角形在七次迭代后，剩余区域的面积计算误差会突破工程允许范围。这提醒研究者，理论模型必须结合实际制造精度进行调整，不能盲目依赖数学理想化模型。

拓扑变换的守恒特性

在橡皮泥般的连续变形过程中，面积平分线展现出惊人的稳定性。莫斯科大学几何实验室的仿真实验证实，即便将正方形扭转为复杂曲面，只要保持拓扑结构不变，初始平分线对应的曲面仍能分割出相等面积。这项发现在医学影像处理中具有重要价值，CT扫描图像的三维重建就依赖此类几何变换。

但守恒定律存在严格边界条件。当图形出现撕裂或粘合时，原有的平分关系将被彻底打破。加州理工学院的研究团队发现，在高温超导材料的晶格缺陷分析中，必须建立新的分割模型才能准确描述电子云的分布状态。

工程实践中的误差控制

上海中心大厦的阻尼器安装位置选择，本质上是寻找建筑截面的质量中心。工程师采用激光扫描结合有限元分析，将数百吨的调谐质量阻尼器定位在误差不超过3厘米的位置。这种精度要求推动着分割算法持续优化，最新的BIM技术已能实现毫米级定位。

在航空航天领域，燃料箱的对称分割直接影响飞行稳定性。SpaceX的猎鹰火箭采用动态平衡系统，通过实时监测燃料消耗情况，自动调整发动机推力分布。这种将几何分割原理与智能控制结合的技术，代表着现代工程的发展方向。

上一篇：乳糖不耐受和食物过敏导致的腹泻如何区分
下一篇：二分之一数据保留对长期趋势预测的可信度验证

---